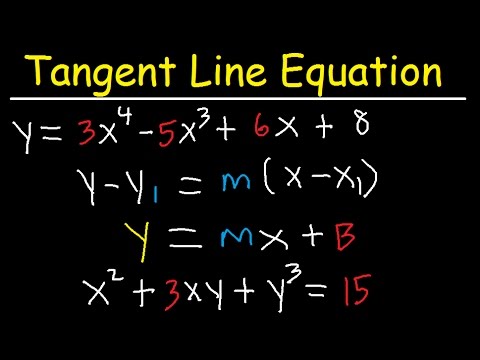When The Tangent Line Is Horizontal

We'll also look at where to find vertical tangent lines, and where to find horizontal tangent lines, since that's something you'll be asked to do often. Horizontal tangent lines exist where the derivative of the function is equal to 0, and vertical tangent lines exist where the derivative of the function is undefined. In terms of the W function, which was developed specifically to solve equations of this type.

While there does exist a general algebraic method for computing derivatives, there is no general algebraic method for solving equations. Even for polynomials, it is known that there can be no generally useful algebraic method of finding roots (i.e., there can be no analog of the quadratic formula) for degree five or above. This is why it is often necessary to resort to numerical approximation methods to solve algebraic equations. The formulas above fail when the point is a singular point. In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. Since any point can be made the origin by a change of variables this gives a method for finding the tangent lines at any singular point.

We can utilize these differentiation techniques to help us find the equation of tangent lines to various differentiable functions. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus. For any constant C, we see that all the tangent line segments along this line have the same slope, no matter what the value of the independent variable, say t.

Another way to look at this is to realize that we can generate infinitely many solutions by taking any one solution and translating its graph left or right. Even when we can't solve an equation, an analysis of its slope field can be very instructive. However, such a graphical analysis may miss certain important features of the integral curves, such as vertical asymptotes.

The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. The graph of z1 shown in Lesson 13.1 suggests that one branch of the curve has a horizontal tangent at and another branch has a vertical tangent at .

Determine the \(x\)-\(y\) coordinates of the points where the following parametric equations will have horizontal or vertical tangents. Using implicit differentiation find y', so that you have a formula for slopes of tangent lines to the graph of the original function. Therefore, when the derivative is zero, the tangent line is horizontal. To find horizontal tangent lines, use the derivative of the function to locate the zeros and plug them back into the original equation.

The tangent at A is the limit when point B approximates or tends to A. A horizontal tangent line is a mathematical feature on a graph, located where a function's derivative is zero. This is because, by definition, the derivative gives the slope of the tangent line. A tangent of a curve is a line that touches the curve at one point. It has the same slope as the curve at that point. A vertical tangent touches the curve at a point where the gradient of the curve is infinite and undefined.

A horizontal tangent line is a mathematical feature on a graph, located where a function's derivative is zero. So in this sense, calling it a tangent line seems reasonable. However, the red line also intersects the curve in two places, which suggests the reverse if we adhere to the old geometric definition of a tangent line. This video explains how to determine the points on a polar curve where there are horizontal and vertical tangent lines. Note that where functions have vertical tangent lines, they are not differentiable at that point. Let us finish by recapping some of the things we covered when finding the equations of tangent lines and normal lines to curves.

Newton's method (also called the Newton–Raphson method) is a way to find x-intercepts of functions. In other words, you want to know where the function crosses the x-axis. The method works well when you can't use other methods to find zeros of functions, usually because you just don't have all the information you need to use easier methods. A horizontal tangent line is parallel to the x-axis and shows where a function has a slope of zero. You can find these lines either by looking at a graph or by setting an equation to zero to find maximums and minimums.

In mathematics, particularly calculus, a vertical tangent is a tangent line that is vertical. Because a vertical line has infinite slope, a function whose graph has a vertical tangent is not differentiable at the point of tangency. Knowing the slopes of tangent lines at various points on the graph of a function can help one better understand the graph of the overall function. At most points, the tangent touches the curve without crossing it . A point where the tangent crosses the curve is called an inflection point.

The study of curves can be performed directly in polar coordinates without transition to the Cartesian system. The values at these points correspond to vertical tangents. If the right-hand side differs from the left-hand side, then a vertical tangent is confirmed. One method to find the slope is to take the derivative of both sides of the equation with respect to x. When taking the derivative of an expression that contains y, you must treat y as a function of x.

This method is called implicit differentiation and it is illustrated below. Find the equations of the horizontal tangent lines. Tangent and secant lines can both be used to find the slopes of curves. Learn more about the differences between the slopes of tangent and secant lines by using them to compare average and instantaneous speeds. The derivative (dy/dx) will give you the gradient of the curve. Find a value of x that makes dy/dx infinite; you're looking for an infinite slope, so the vertical tangent of the curve is a vertical line at this value of x.

Once you have the slope of the tangent line, which will be a function of x, you can find the exact slope at specific points along the graph. The instantaneous rate of change is the slope of the tangent line at a point. A derivative function is a function of the slopes of the original function. The vertical tangent to a curve occurs at a point where the slope is undefined . This can also be explained in terms of calculus when the derivative at a point is undefined.

The tangent plane to a surface at a given point p is defined in an analogous way to the tangent line in the case of curves. The angle between two curves at a point where they intersect is defined as the angle between their tangent lines at that point. More specifically, two curves are said to be tangent at a point if they have the same tangent at a point, and orthogonal if their tangent lines are orthogonal. A cusp corresponds to a "corner" or abrupt change in direction of a curve representing a function that is continuous at the point in question.

The curve has different tangents immediately to the right and left of a cusp. The derivative has many applications in "real life"; one of the most useful is to find the rate of change of one variable with respect to another. Think of a rate of change, or sometimes called an instantaneous rate of change as how fast something is changing at a certain point, like a point in time. Vertical tangent lines occur at the points (-4, -1) and (2, -1). No, the curve cannot have a horizontal tangent where it crosses the x-axis.

Use a straight edge to verify that the tangent line points straight up and down at that point. If the right-hand side of the equation differs from the left-hand side , then there is a vertical tangent line at that point. 2) Plug x value of the indicated point into f ' to find the slope at x.

3) Plug x value into f to find the y coordinate of the tangent point. 4) Combine the slope from step 2 and point from step 3 using the point-slope formula to find the equation for the tangent line. In this question, we want to find the tangent to a curve which makes an angle of 135∘ with the positive 𝑥-axis. This means that to answer this question we are going to need to work out the corresponding slope for the line that makes this angle with the positive 𝑥-axis. When 𝑓 is not differentiable at a point, sketching the graph can often help us determine whether this point has a vertical tangent line.

In this explainer, we will learn how to find the slope and equation of the tangent and normal to a curve at a given point using derivatives. A tangent line is a linear function that intersects a curve at one point only. The horizontal tangent line is an equation whose slope is equal to zero.

The slope of the tangent line is given by the first derivative of the equation of the curve. The next topic that we need to discuss in this section is that of horizontal and vertical tangents. We can easily identify where these will occur (or at least the \(t\)'s that will give them) by looking at the derivative formula. A tangent line is a line that touches a graph at only one point and is practically parallel to the graph at that point. It is the same as the instantaneous rate of change or the derivative .

You can find the instantaneous rate of change of a function at a point by finding the derivative of that function and plugging in the x -value of the point. Any two variables can be related in a similar way. In each case, the slope of the tangent line corresponds to the rate of change in one variable seen for a particular value of the other. Understanding the nature of slopes of tangent lines to functions can raise red flags when appropriate to alert us to not be so quick to believe what we see on our calculator screens. These methods led to the development of differential calculus in the 17th century. Further developments included those of John Wallis and Isaac Barrow, leading to the theory of Isaac Newton and Gottfried Leibniz.

In the differential equations and dynamic optimization, where the independent variable is the time. The solutions to the system can be found by using the Solve command to find values for the two variables x and y that make both equations true. Notice that parentheses are used to indicate that z1 is a function of x and y and that the variables to be found, x and y, are enclosed within braces. First, if we translate a line, it will not change the angle it makes with the positive 𝑥-axis. So, we can start by sketching our line passing through the origin , making an angle of 135∘ with the positive 𝑥-axis.

This will have the same slope as our tangent line. We want to find the 𝑥-coordinate where the tangent line to this curve will be parallel to the 𝑥-axis. We know that the 𝑥-axis is horizontal, so any line parallel to this must also be horizontal; in other words, the slope of this tangent line must be equal to zero. Finding the equation of the normal line will take a little bit more work since the derivative of the function only gives us the slope of the tangent line. To find the equation of the normal to a curve at a point, we need a point on the line and its slope to find the point-slope equation. Well, recall from your Calculus I class that with the second derivative we can determine where a curve is concave up and concave down.

We could do the same thing with parametric equations if we wanted to. To find the points at which the tangent line is horizontal, we have to find where the slope of the function is 0 because a horizontal line's slope is 0. Now set it equal to 0 and solve for x to find the x values at which the tangent line is horizontal to given function. In calculus, differential approximation is a way to approximate the value of a function close to a known value.

It is just another name for tangent line approximation. In other words, you could say "use the tangent line to approximate a function" or you could say "use differentials to approximate a function"; They mean the same thing. Find a value of x that makes dy/dx infinite; you're looking for an infinite slope, so the vertical tangent of the curve is a vertical line at this value of x. To find the points at which the tangent line is horizontal, we have to find where the slope of the function is 0 because a horizontal line's slope is 0. In the discussion above, we refer repeatedly to a tangent line to a function at some point.

In geometry, one normally defines a tangent as a line that intersects a curve at only one point. Suppose that the $x$-axis now represents time, and the $y$-axis represents the position/height of some object -- perhaps a rising red balloon. The slope of the tangent line is then a distance traveled divided by an elapsed time and can thus be interpreted as a velocity. Using the limit defintion of the derivative, find the equation of the line tangent to the curve at the point .

An 1828 definition of a tangent was "a right line which touches a curve, but which when produced, does not cut it". This old definition prevents inflection points from having any tangent. It has been dismissed and the modern definitions are equivalent to those of Leibniz, who defined the tangent line as the line through a pair of infinitely close points on the curve. A tangent is a line that intersects a curve at only one point and does not pass through it, such that its slope is equal to the curve's slope at that point.

To find a horizontal tangent, you must find a point at which the slope of a curve is zero, which takes about 10 minutes when using a calculator. We need to know that the derivative is infinite atto have a vertical tangent. We can see this from the graph, so we have a vertical tangent at. Notice that the derivative is of the form 0/0 at . A vertical line has undefined slope because all points on the line have the same x-coordinate. As a result the formula used for slope has a denominator of 0, which makes the slope undefined..

Tangent, in geometry, straight line that touches a given curve at one point; at that point the slope of the curve is equal to that of the tangent. A tangent line may be considered the limiting position of a secant line as the two points at which it crosses the curve approach one another. C) If the line is tangent to the curve, then that point on the curve has a slope of -1. If 𝑓′(𝑥) is undefined, we may still be able to find the tangent and normal lines at 𝑥. Two curves intersect orthogonally at the point (𝑥,𝑦) if both curves intersect this point and the slopes of their tangents at this point are orthogonal.

We say that two curves intersect orthogonally if they intersect at right angles. Equivalently, the tangent lines to both curves at the point of intersection are orthogonal . In our next example, we will find the equation of a tangent line to a curve that makes a specific angle with the positive 𝑥-axis. This gives us an equation to find the slope of our normal line; it is the negative of the reciprocal of the slope of the tangent line.

We also know how to find the slope of the tangent by using the derivative. However, there is another important type of line we need to consider called a normal line. A normal line to a curve at a point is very similar to the tangent line; the only difference is that the normal line will be perpendicular to the tangent line. Implicit differentiation is a technique used to find derivatives if the function is not easily expressed as a function of a single variable.

Can I Download Windows 10 On Mac For Free

In addition to installing Windows alongside macOS on your hard drive, you can also run Windows in a virtual machine directly from macOS. This way, you can easily access both operating systems at the same time and transfer files between them without restarting your Mac. Installing macOS on a Windows computer is tricky, but not impossible. Once you've installed macOS, it's a good idea to run Multibeast from the flash drive in order to install drivers needed for things like sound, Internet, and graphics cards.

What about Boot Camp, Apple's long-standing option for running a Windows system on a separate partition on an Intel-based Mac? Boot Camp still exists, but Apple has effectively stopped supporting it. And Boot Camp has a major inconvenience; you have to shut down your macOS system and restart it every time you want to run Windows. There's no integration between macOS and your Windows partition, either. Boot Camp won't let you run a Mac app and a Windows app at the same time or transfer files between systems quickly, for example. If you have an Apple Silicon Mac, don't even think about Boot Camp.

If you want to run complex software such as the Windows version of Excel or any high-end game, then you need to set up a virtual Windows system, sometimes known as a virtual machine . You can run this virtual system entirely inside a macOS app. The VM behaves as if it's running on real hardware with a real hard drive; it just runs a bit slower than a Windows system running on physical hardware.

The reason for the slower performance is that this method requires you to run an entire Windows system in the background in addition to the app you want to use. Boot Camp doesn't allow you to easily transfer content between OS X and Windows partitions like virtual machines do, and you can't run the two operating systems simultaneously. But it does give Windows full access to the processing power of your Mac. It's also completely free , and a shared Dropbox / Google Drive / OneDrive folder can make data transfers a bit easier. Regardless of whether you choose Parallels or VMWare, set aside about 20 minutes to install Windows and 30GB or more of disk space on your system. If you wish to run both macOS and Windows on a single Mac computer, UITS recommends using Apple's Boot Camp utility to install Windows 10 on your Intel-based Mac.

Saving the state of your macOS virtual machine session is easy. With this release, Windows is back on the Mac, but with a big caveat. The software requires that you use a version of Windows designed to run on ARM processors, called Windows 10 for ARM64. Both Parallels and VMware Fusion let you create a virtual system by cloning an existing desktop system across a network, but it's a lot simpler to install a fresh copy of Windows. Users of Intel-based Macs can download the standard Windows ISO file from Microsoft and rely on Parallels or Fusion to install Windows correctly from there. M1 Mac users must register for the Windows Insider Preview program and download the ARM version of Windows 10.

Only Parallels supports the ARM version, but it has no trouble configuring your Windows VM with that version on an Apple Silicon Mac. Parallels recently announced support for Windows 11 on M1 Macs, but again, for the ARM version only. You need to have a version of macOS for clover to work, because then you can get the install program that you put on a flash drive .

However, this doesn't necessarily mean that you are stuck. I would recommend option a) as it is the easiest, safest, and most legal option, as well as the fact that you are using the latest real version of macOS. On an Apple Silicon-based Mac , Parallels Desktop is your top option. Parallels is more approachable for beginners and faster. VMware Fusion is friendly enough for any experienced Windows or Mac user, but it's more suitable for corporate use.

Next, download and install Parallels Desktop if you don't already have it. At the end of the installation, the program tells you that you need an installation image with an ARM-based operating system. Click the link for "How to download Windows 10 on ARM Insider Preview" for documentation and a video that explain the process. At the Create New screen, click the button for "Install Windows or another OS from a DVD or image file." Click Continue . Microsoft just didn't officially allow you to download Windows without a product key, and there was no way to fully upgrade to a licensed system from within Windows.

It's like a free demo, and you can use it to make all the virtual machines you like for testing purposes. Although there are other virtual machines are available, Parallels is by far the easiest way to install Windows 10 on Mac. Parallels has been around for many years and the installation process in the latest version of Parallels is now so automated and refined then it even downloads and install Windows 10 for you. You don't even need to purchase it to try it – you can download a free trial of Parallels instead. VirtualBox is a powerful program to create a virtual machine and install operating systems on it.

It is one of the best choice to run Mac on your Windows PC for free. Just download it from the official site and install it on your PC. Then, create a virtual machine and install Mac on it.

Both Mac and Windows have different features and different programs. Sometimes, users need to use Mac programs to do their work, which is not possible on Windows. You can create a dual-bootable computer on your PC by installing both Mac and Windows.

Due to the nature of the configuration of the virtual machines, the update process is not the same as a regular macOS installation on proper hardware. The patches and workarounds that make the macOS virtual machine work with a particular version may not work with the update. The above tutorial will guide you through the virtual machine download and installation process, how to download the macOS operating system, and how to install it on the virtual machine. There are two easy ways to install Windows on a Mac. Just begin the installation process and install Windows 10 like you normally would. You may be asked to enter a product key later in the process, too–if you are, just look for a similar small link to skip that screen.

Perhaps the easiest way to get Windows up and running on your Mac is to use virtual machine software. No, unfortunately, it's not possible to install the x86 version of Windows on Macs powered by the Apple M1 chip, which is an ARM-based system on a chip. VMware is currently working on M1 support and expects to deliver virtual machines on Apple silicon in the near future.

You can purchase a Windows 10 Activation key and activate Windows, or you can sign up to the Windows Insider Program. The downside of joining the Windows Insider program is that you'll be running prerelease versions of Windows 10, which could possibly come with stability issues. Activating the Windows Insider Program on your installation also means that you're willing to deliver usage data to Microsoft and its partners. The upside of the Windows Insider Program is that it provides you with a genuine activation without having to pay out of pocket.

Boot Camp is also referred to as dual-booting that makes you run macOS and Windows on a single hard drive side by side. This method offers better performance as compared to virtual machines as Windows can leverage all the resources of the system. I'm already working with React Native and in Xcode using my own mac, but in the company I work, I'm using windows and I think Virtual Box is the better option.

Other option i used in another company I worked for was Ionic (it's the mobile friend of angular like React native is the mobile friend of React). Choose Runafter the download to make sure your hardware is compatible. Then Accept and Install to agree to the licensing terms and begin the installation.

When the program is finished installing, you'll be prompted to restart your computer. Your PC might restart several times during the process of finishing the installation, so don't be alarmed. During this part of the installation, your Mac will restart a few times, ultimately landing you at a screen that will ask you which partition you want to install Windows 10 on. Select the partition labeled "Boot Camp," format it for NFTS, and continue with the installation.

You'll go through the setup wizard where Windows will ask you for the product key and you'll be on your way. Right now, the easiest, cheapest, and fastest way to get Windows 10 on your Mac is Boot Camp, and that's what we're using for this tutorial. The first thing you should do is check the system requirements to make sure your Mac can actually run Windows 10. Your Mac needs at least 2GB of RAM and at least 30GB of free hard drive space to properly run Boot Camp. You'll also need at least a 16GB flash drive so Boot Camp can create a bootable drive to install Windows 10. Make sure you have at least 64GB of free space on your hard drive for the Windows installation.

During the installation process, you can set the Windows partition to whatever size you want, as long as the drive has enough storage. Apps won't run as quickly or as smoothly as they do with commercial solutions, and you still need to purchase a Windows license to use with VirtualBox. Close the configuration window and click Continue. After the installation, click the Windows 11 screen to continue. Windows 11 opens as a virtual machine inside Parallels Desktop. Once Boot Camp Assistant creates the partition, it asks for your administrator password.

Your Mac then restarts and loads the Windows ISO. Follow the steps in the ISO's installer, entering your product key and choosing the correct version of Windows to install. If your copy of Windows came on a USB flash drive, or you have a Windows product key and no installation disc,download a Windows 10 disk image from Microsoft. JohnIL February 12, 2021 I prefer to run Windows natively, I use Windows 10 a lot on my Mac's. Apple moving to a custom ARM chip for Mac's means that Boot Camp is no more.

Parallels is working on a M1 Mac based preview but even that application will only run ARM based operating systems. I think Apple switched to its chips purely on locking in users and making more profits. I have my doubts since the whole platform becomes locked to Apple. SFTP With support for strong ciphers, public key and two factor authentication. Read settings from your existing OpenSSH configuration. WebDAV With interoperability for ownCloud, box.com, Sharepoint and BigCommerce and many other WebDAV servers.

TLS mutual (two-way) authentication with client certificate. OpenStack Swift Connect to Rackspace Cloudfiles or any other OpenStack Swift cloud storage providers. Google Cloud Storage Connect to buckets in Google Cloud Storage and configure as a website endpoint.

On the other hand, dual booting doesn't allow Windows and macOS to run at the same time, so it's not suitable for users who need to use the two operating systems simultaneously. VirtualBox users also have the option to take a snapshot. A snapshot saves the virtual machine's current state, allowing you to create a string of snapshots as you use Apple apps and the macOS operating system.

CrossOver is simple to set up with 1-click installation and use applications at top speed. Available at a starting price of just $39.95, the software is an economical choice. It also saves plenty of your computer resources and occupies only the space the Windows programs need while saving you from hassles of rebooting. Before Apple silicon, Mac users could install a copy of x86 Windows 10 using Apple's Boot Camp or through virtualization. Under the new system, Boot Camp has been removed, as has x86 compatibility.

Installing Windows 10 on M1 Macs requires an ARM copy of Microsoft's operating system. At the time of this writing, Microsoft only offers a copy through its ARM Insider Preview program, which features a beta version of Windows. Open up Boot Camp Assistant, which can be found in the Utilities folder in your Applications list. Boot Camp will prompt you to back up your Mac, which you should have already done. The next page will ask you to select the tasks you want Boot Camp to complete. Check all the boxes, make sure your flash drive is plugged in, and click continue.

Select the Windows 10 ISO location , and choose the USB drive as the destination, and click Continue. Boot Camp will create a boot drive with all of the necessary drivers. The Tools tab in your Wineskin app also has a button that launches an app called Winetricks; it lets you install fonts your app may need or change the emulated Windows version. In the Wineskin app's Configuration tab, you can replace the default Wineskin app icon with any icon you choose.

Expert Windows users can use the Regedit button to modify the Wine version of the Windows registry so that a Wine-based app will open files dropped on it. A few minutes with Regedit were enough to modify my Axialis app so that it automatically opened any Mac icon I dropped on it. You can find instructions for modifying the Registry on the web, for example, method 4 on this page. Depending on the app or game container you build, you may need to customize it so that it can access folders on your Mac system. Don't try to open the newly created app yet—you'll get an error message. Instead, right-click it and select Show Package Contents.

In the Finder window that opens, double-click the Wineskin app (this is the only part of the system that's simply called Wineskin). Choose Install Software, then Setup Executable, and navigate to the installer for your software. I had already downloaded the Axialis installer for my example, so I chose that from my Mac's Downloads folder. For example, I installed the Windows text editor Notepad++ with a few clicks and opened it instantly.

For instance, I tried to install Axialis IconWorkshop, the best Mac icon editor that I've found (which also happens to be Windows-based), from CrossOver's menus. No matter what I tried, the Install button remained grayed out. Eventually, I was able to install the app manually, but doing so wasn't easy and I don't recommend you try that process. Parallels starts to create the virtual machine for Windows 11. Click the category for Hardware and select CPU and memory. Make sure that at least two CPUs are selected and then change the memory to at least 4GB .

At the next screen, enter the license key for Windows 11. Uncheck the box for Enter Windows License Key for faster installation if you wish to bypass this for now. At the next screen, select the edition of Windows 11 that you want to install, such as Windows 11 Home or Windows 11 Pro. First, you'll need to download the ISO file for Windows 11 on your Intel-based Mac.